
今回はpythonで定積分の近似をしていきたいと思います。数学チックですね。
、、、、。この時点で読む気なくした方は、せっかくですので他のページにでも寄ってってください。
8月から和菓子屋さんも始めました(笑)
お餅のとけしをオープンしました。
北谷にくる際はぜひつ。
定積分とはなんなのか
定積分とは,不定積分に積分区間を定めたもので対象関数の
特定範囲の面積を表します。
例えば次の関数の面積を求めてみましょう。
$$ y = -x^2 + 9 $$
条件は( \(y > 0\))の時、( \(-3 < 0 < 3\))の範囲とします。
グラフは次のような形になります。
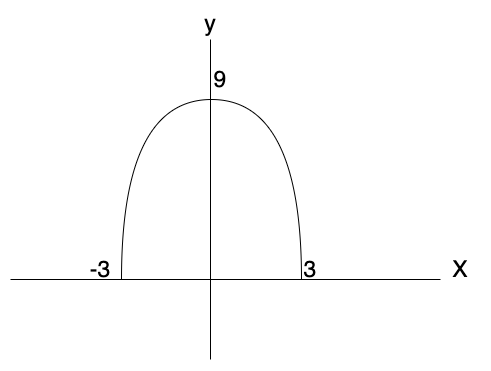
今回の問題では求めるのは次の図の赤い部分です。
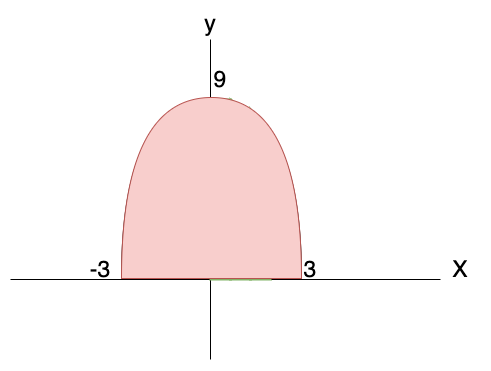
実際の計算は次のようになります。
$$ \int -x^2+9 dx $$
$$ =-\int x^2 dx + 9\int 1 dx $$
$$ =-\frac{x^3}{3} + 9x $$
上記不定積分の結果を用いての \(x\)に \(-3\)と \(3\)を
代入して計算すると \(36\)の結果が得られます。
Pythonのライブラリを用いて定積分を実行してみる
pythonで積分を実行する場合SymPyというライブラリを
用いて下記のようなプログラムを記述することで、定積分を求めることが可能なんですね~。
|
1 2 3 4 5 6 |
from sympy import * x=Symbol('x') y=Symbol('y') #-1*x**2+9の定積分 integrate(-1*x**2+9, (x,-3,3)) |
実行結果
|
1 |
36 |
簡単です!
次はライブラリを利用せず積分の概念をプログラム化して
定積分の値を近似してみます。
Pythonと区分求積法で面積を求める。
区分求積法とは、文字の通り区分されたものを積み上げる方式です。
先ほどのグラフを例とすると次のようになります。
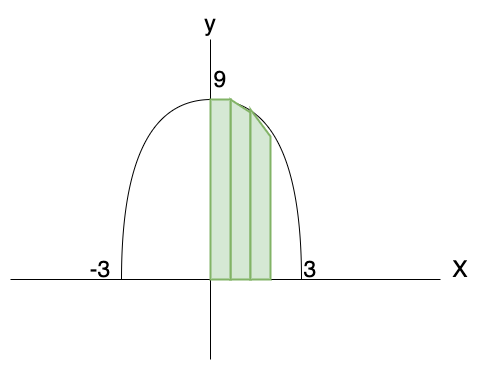
緑の四角(台形)をグラフをはみ出さないように配置していきます。
配置後、全ての台形の面積の総和がこの関数の面積になることは想像しやすい
かと思います。
もちろん、滑らかな曲線なので完全に台形とグラフは一致せず誤差が生じますが
この台形の横幅を細かくすることでその誤差を低減させることができます。
ということでこの仕組みをプログラム化していきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
#台形の横幅(高さ)を定義 interval = 0.1 #積分範囲の開始値(x) start = -3.0 #積分範囲の終了値(x) end = 3.0 #現在の台形の計算位置 current = start #関数の係数を定義 (y = ax^2 + bx + c) a = -1.0 b = 0.0 c = 9.0 #関数の計算結果(y)を算出する関数 #※台形の上辺と下辺を計算する関数 def calcYval(x): return a * x **2 + b*x + c #定積分を近似する関数 def calc(start, end, current): #面積値を保存する変数 result = 0 #繰り返し処理 while True: #heightにintervalを代入する height = interval #top(上辺)にx=current時のy値を代入 top = calcYval(current) #bottom(下辺)にx=current+interval時のy値を代入 bottom = calcYval(current + interval) #resultに台形の面積を加算していく result = result + (top + bottom) * height / 2 # resultをinterval分進めて次の台形を計算対象とする。 current = current + interval # currentが積分範囲以上の場合はループを抜ける if current >= end: break #結果を表示 print(result) #定積分を近似するプログラムを実行する calc(start, end, current) |
ちょっとわかりにくいのですが図示すると次のようになります
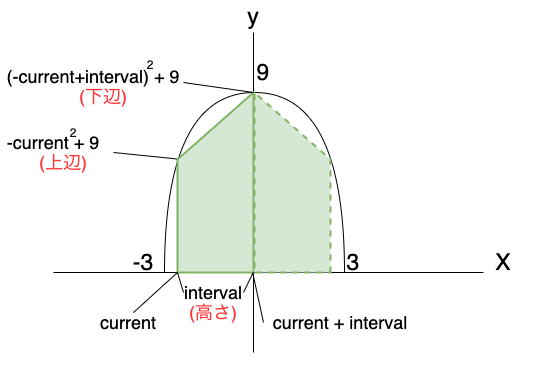
intervalが高さ、 \( y = -x^2 + 9 \)のxにcurrentをいれた値が
上辺、current+intervalをいれた値が下辺となります。
つまり、台形を細かくすることはintervalの値を小さくしていくこととなります。
実際に動作を確認してみましょう。
interval = 0.1の場合
|
1 |
35.98999999999998 |
この時点でほぼ36がでていますが
intervalをさらに小さくして結果をみていきましょう。
interval = 0.01
|
1 |
35.999599500000066 |
interval = 0.001
|
1 |
35.99999599950215 |
interval = 0.0001
|
1 |
35.99999998999126 |
intervalを小さくするに従って36に近づくことがわかると思います。
同じ方法で円の面積を求めることができるので是非挑戦してみてください!




